SCALP - Scaling and Simulation of Alpine Precipitation
Dates: 2009-2013
Funding: Swiss National Science Foundation
PhD Student: Athanasios Paschalis
Principal Investigator: Peter Molnar, Paolo Burlando
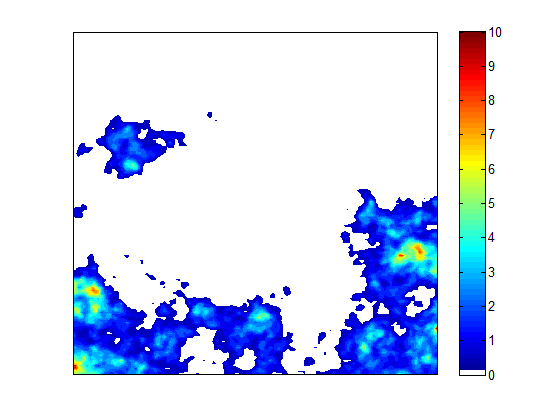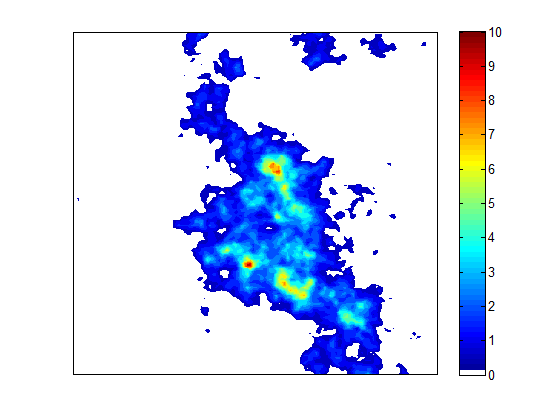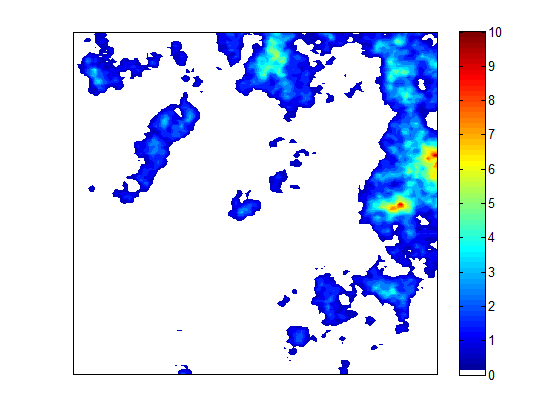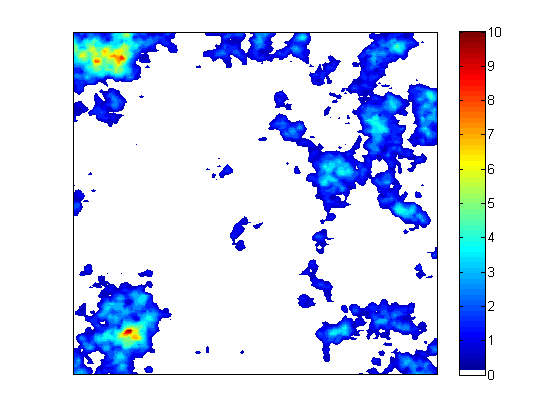
Precipitation in mountainous regions is highly variable in space and time due to the complex effects of orography on storm generation and advection. In this project we investigated the statistical properties of precipitation from small point scales (raingauge) to large scales (weather radar) in the Swiss Alps, and the ways in which they can be utilized for precipitation simulation. To this end we first studied the properties of temporal rainfall and their modelling by random cascades. We then developed a new space-time stochastic rainfall simulator STREAP and used it to quantify the effects of rainfall on flood peaks and timing. Finally we tested a nested approach combining point process models and random cascade disaggregation to simulate high resolution temporal stochastic rainfall time series suitable for impact studies in urban hydrology and other fields.
The outcomes of the research were recognized by the American Geophysical Union AGU Editor's Choice Award for outstanding paper in 2014 in Water Resources Research.
The model STREAP is part of the 2-dimensional weather generator AWE-GEN-2D, which combines physical and stochastic approaches to simulate key climate variables, precipitation, cloud cover, near-surface air temperature, solar radiation, vapor pressure, atmospheric pressure and near-surface wind, at high resolutions in time (min) and space (m-km). More about AWE-GEN-2D can be found here.
Temporal dependence in random cascade weights
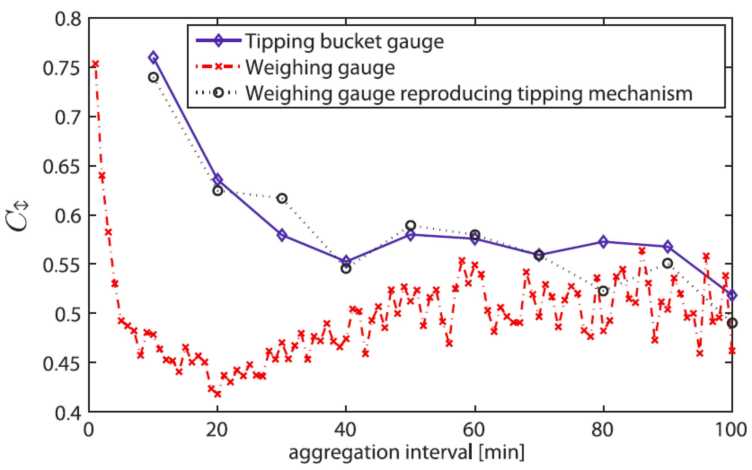
We investigated the effect of the dependence structure in cascade weights due to clustering and within-storm variability on the temporal correlation in precipitation simulated by the multiplicative random cascade disaggregation model with data from 69 stations with 10 min precipitation records in Switzerland. Correlation was quantified with the oscillation coefficient, which is a measure of patterns of fluctuations in data. We showed that the assumption of temporal independence in cascade weights is generally not supported by observations at 10-min to 1-hr resolutions, which show generally higher correlation than the simulations produced with the cascade model with independent weights. Seasonal effects and measurement artefacts (e.g. the aggregation by a tipping bucket instrument) are also apparent and important. Only at scales coarser than 1-hr the assumption of temporal independence in weights is acceptable.
Paschalis, A., P. Molnar, and P. Burlando (2012), external page Temporal dependence structure in weights in a multiplicative cascade model for precipitation, Water Resour. Res., 48, W01501, doi:10.1029/2011WR010679.
Stochastic space-time precipitation model STREAP
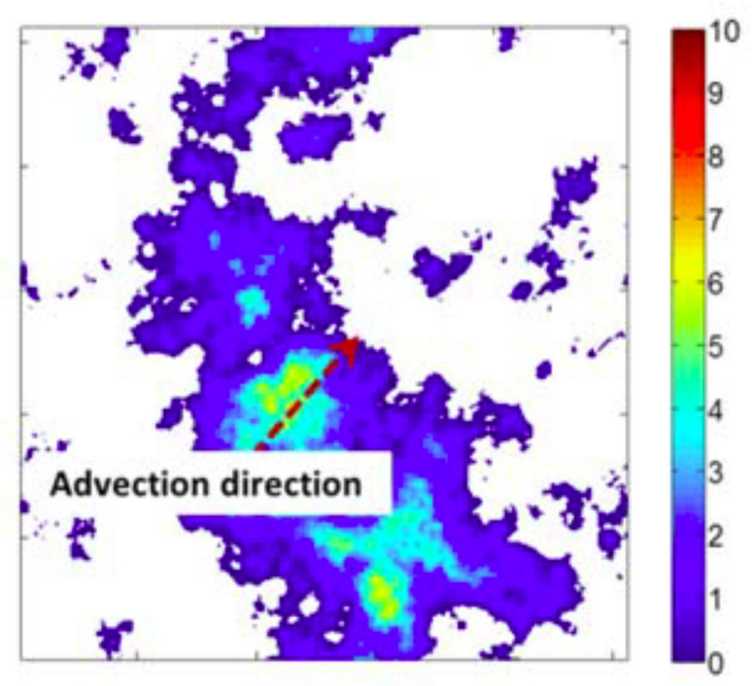
In this research we developed a new high-resolution space-time stochastic model for precipitation STREAP for continuous simulation. The
model is based on a three stages hierarchical structure that mimics precipitation formation: (a) the storm arrival process, (b) the temporal evolution of areal mean precipitation intensity and wet area, and (3) the evolution in time of the two-dimensional storm structure. Each stage of the model is based on appropriate stochastic modelling techniques spanning from point processes, multivariate stochastic simulation and random field simulation with FFT. STREAP was applied to a case study in Switzerland using 7 years of high-resolution (2x2 km2, 5 min) data from weather radars. The model was validated by a wide range of areal and point scale statistics. The results shows that a more accurate description of the space-time structure of precipitation fields in STREAP does indeed lead to a better performance for properties and at scales which are not used in model calibration. An example simulation with the model is shown in the header of this page.
Paschalis, A., P. Molnar, S. Fatichi, and P. Burlando (2013), external page A stochastic model for high-resolution space-time precipitation simulation, Water Resour. Res., 49, 8400-8417, doi:10.1002/2013WR014437.
This paper was awarded the AGU Editor's Choice Award 2014.
Quantifying the effects of rainfall on floods
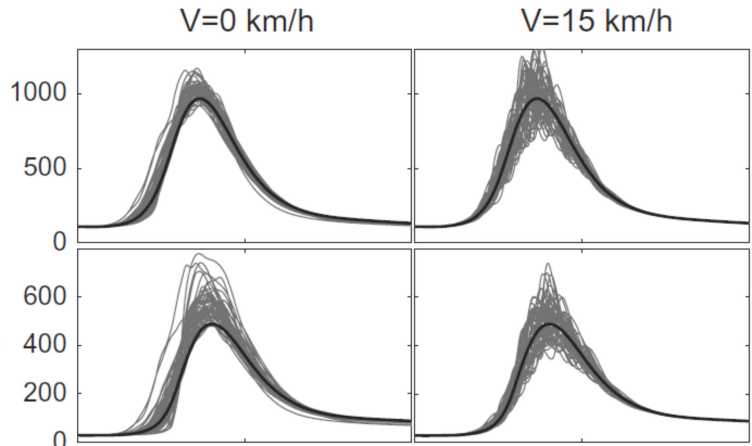
Stochastic rainfall models are particularly suitable tools to study the effects of the space-time rainfall structure on flood peaks and timing. Here we quantified this impact in a numerical study with STREAP and a distributed process-based hydrological model Topkapi-ETH for the Kleine Emme basin in central Switzerland. The results showed that the flood response is strongly affected by the temporal correlation of rainfall intensity and to a lesser extent by its spatial variability. Initial soil moisture conditions play a paramount role. We also showed that the connectivity of saturated areas determines the sensitivity of flood response to the spatio-temporal variability of rainfall, especially for moving storms. The clustering of saturated areas in the catchment led to local enhanced runoff and higher flood peaks. The effect of rainfall on floods will be enhanced in small urban catchments with low infiltration rates and fast runoff response.
Paschalis, A., Fatichi, S., Molnar, P., and Burlando, P. (2014), external page On the effects of small scale space-time variability of rainfall on basin flood response, J. Hydrol., 514, 313-327, doi:10.1016/j.jhydrol.2014.04.014.
Nesting models for temporal rainfall simulation

It is important that stochastic models of temporal precipitation satisfactorily reproduce precipitation properties across a wide range of temporal scales. In this research we nested a disaggregation model at scales less than 1-hr (microcanonical multiplicative random cascade model) into a range of point process models at coarse scales (Alternating renewal processes, Markov chains, Poisson cluster models). The composite nested model combinations were tested on data at four sites in different climates (USA, New Zealand, Switzerland). The results showed that composite models have improved performance in key statistics such as probability distributions of precipitation depth, autocorrelation structure, intermittency, reproduction of extremes, across a wider range of scales than single models alone. The results for the four different climates were similar, which suggests a degree of generality and wider applicability of the approach for the simulation of precipitation timeseries.
Paschalis, A., Molnar, P., Fatichi, S., and Burlando, P. (2014), external page On temporal stochastic modeling of precipitation, nesting models across scales, Adv. Water Resour., 63, 152-166, doi:10.1016/j.advwatres.2013.11.006.